Implémentation des Arbres binaires en Poo¶
Python ne propose pas de façon native l’implémentation des arbres binaires.
On va utiliser la POO pour créer une classe AB (pour Arbre Binaire), en utilisant le caractère récursif d'un arbre: une racine, et éventuellement un sous-arbre gauche et un sous-arbre droit.
| 🐍 Script Python | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | |
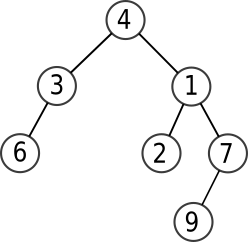
On peut alors créer l'arbre ci-après de cette manière:
| 🐍 Script Python | |
|---|---|
1 2 3 4 5 6 7 | |
Objectif
Dans ce TP, il s'agit d'utiliser l'implémentation POO d'un arbre binaire et d'implémenter des fonctions:
- de calcul de taille
- de calcul de hauteur
- de parcours (largeur, préfixe, infixe, postfixe)
Compléter au fur et à mesure la classe AB.
Stratégie
Dès que possible, il s'agit d'exploiter le caractère récursif de la structure d'arbre pour écrire les méthodes suivantes...
Taille et hauteur
- Écrire une méthode renvoyant la taille d'un arbre binaire.
- Écrire une méthode renvoyant la hauteur d'un arbre binaire.
| 🐍 Script Python | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 | |
```
DFS
Écrire les méthodes prefixe, infixe et postfixe parcourant l'arbre en profondeur d'abord selon les algorithmes correspondants (page précédente). Le traitement de la racine consistera en un affichage (print).
| 🐍 Script Python | |
|---|---|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | |
recherche d'une valeur
Écrire une méthode permettant de déterminer si un arbre contient une valeur donnée. La méthode renverra un booléen selon le résultat de la recherche.
Avec un parcours préfixe adapté:
| 🐍 Script Python | |
|---|---|
1 2 3 4 5 6 7 | |